14 марта не является обычным Днем Пи в этом году. Любители математики повсеместно отмечают это событие как День предельного числа Пи, потому что дата будет соответствовать первым пяти цифрам числа Пи (3.1415), а не только первым трем. Это математическое слияние не возобновится в течение столетия, 14 марта 2115 года.
Связанный контент
- Мир полон кругов
Определяемый как отношение длины окружности к ее диаметру, pi ( π ) является одновременно и трансцендентным, и иррациональным числом, означающим, что оно никогда не может быть записано как отношение двух целых чисел и продолжается бесконечно без повторяющегося шаблона. Пи не единственное иррациональное число - есть, например, число Эйлера (е) и золотое сечение ( φ или фи). Но это продолжает быть источником восхищения, потому что его происхождение легко объяснимо, говорит Марио Ливио, астрофизик из Научного института космического телескопа в Мэриленде.
«Каждый может понять, как происходит пи. Все остальные числа более сложные. Например, число «фи» подразумевает определенное деление линии, а число «е» требует, чтобы вы знали, что такое логарифм », - говорит Ливио, автор книги« Является ли Бог математиком?
Еще одна важная часть привлекательности pi состоит в том, что он обладает необычайным умением появляться в математических формулах, многие из которых важны для повседневных процессов, от обработки изображений до GPS-навигации. Вот лишь небольшая выборка часто используемых формул, которые включают в себя пи:
Преобразование Фурье
Названный в честь французского математика Жана-Батиста Жозефа Фурье, этот математический инструмент разбивает сигнал на составляющие его частоты - подобно тому, как музыкальный аккорд можно разбить на ноты его компонентов. По сути, преобразования Фурье идеально подходят для обработки основанных на волнах сигналов, таких как звук или свет, и для поиска шаблонов. Это делает преобразование Фурье фундаментальным инструментом в современном цифровом мире.
«Он был назван самым важным алгоритмом, когда-либо разработанным человечеством. Теперь это может быть гиперболой, но, возможно, это не так », - говорит Глен Уитни, основатель и директор Национального музея математики в Нью-Йорке. Преобразования Фурье используются постоянно для очистки цифровых изображений, для автоматической настройки поп-звезд и для поиска отдаленных планет, вращающихся вокруг других звезд. Этот инструмент также важен для функций преобразования голоса в текст, которые в настоящее время являются стандартными для смартфонов. «Когда вы используете Siri или Google Now, один из первых шагов - это взять свой голос и выполнить преобразование Фурье на нем… Оказывается, намного легче распознать гласные, когда вы смотрите на их преобразования Фурье, чем когда вы смотрите на сами по себе оригинальные сигналы », - говорит Уитни.
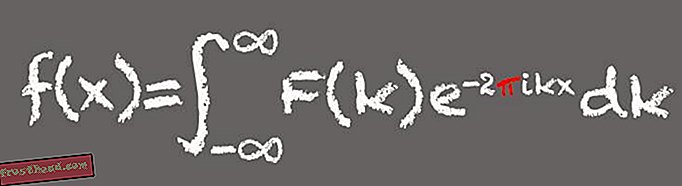(Иллюстрация Виктории Джаггард) Pi появляется в преобразовании Фурье, потому что одна из составных частей или выражений формулы связана с синусом и косинусом и углами, созданными частицей, путешествующей по кругу. «Всякий раз, когда у вас есть формула, которая имеет дело с кругами или углами, вы не удивитесь, когда появится пи», - говорит Уитни.
Принцип неопределенности Гейзенберга
Один из столпов квантовой механики, принцип неопределенности Гейзенберга, гласит, что наблюдатель не может знать одновременно положение и скорость субатомной частицы одновременно. Вместо этого, чем точнее известно положение частицы, тем меньше можно знать о ее скорости.
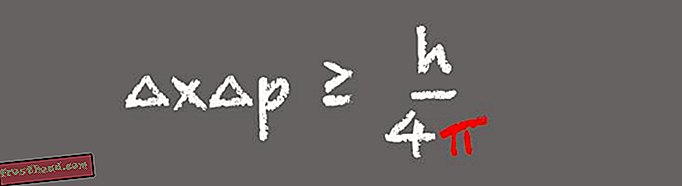(Иллюстрация Виктории Джаггард) По словам Уитни, появление пи в принципе неопределенности Гейзенберга имеет смысл, когда вы понимаете, что в формуле позиция и импульс являются преобразованиями Фурье друг друга. Принцип неопределенности важен в современном мире, потому что он описывает поведение легких частиц или фотонов в волоконно-оптических системах связи. «Это говорит нам о том, что мы не можем знать как положение, так и импульс фотонов с предельной точностью. Вы не можете разработать протоколы связи, которые нарушают принцип неопределенности Гейзенберга, потому что они не будут работать ».
Закон Стокса
Закон Стокса вычисляет силу, необходимую для перемещения небольшой сферы, то есть трехмерного круга, через вязкую жидкость с определенной скоростью. У этого есть заявления в областях, варьирующихся от наук о Земле до медицины.
(Иллюстрация Виктории Джаггард) «Закон конкретно касается влияния вязкости на сферу во флюиде», - говорит Уитни, и именно так в игру вступает пи. Что касается практического использования закона Стокса, смотрите не дальше, чем ваш автомобиль. «В течение десятилетий компании проверяли, чтобы ваше моторное масло имело правильную вязкость для вашего автомобиля, буквально капая серию испытательных шариков в масло и измеряя время, необходимое им, чтобы провалиться сквозь жидкость», - говорит Уитни. Сегодня наиболее распространенный способ измерения вязкости масла включает в себя инструмент, называемый вискозиметром с капиллярной трубкой, без сфер, но он по-прежнему сообщает результат в единицах измерения, называемых сантистоксами.
Формула Эйлера
Названная в честь швейцарского математика Леонарда Эйлера версия этой формулы, в которую входит пи, собирает некоторые из самых интригующих чисел в математике в одном месте:
(Иллюстрация Виктории Джаггард) «Все просто думают, что это невероятно. Все эти числа, которые мы считаем специальными, появляются в одном прекрасном уравнении », - говорит Ливио. Хотя эта содержательная формула может внушать благоговение математикам, более полезная форма уравнения немного длиннее:
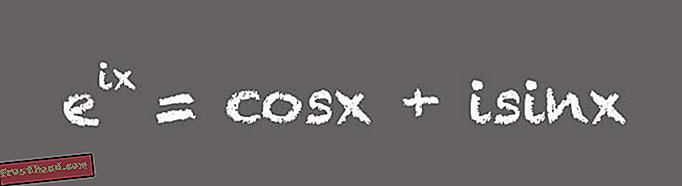(Иллюстрация Виктории Джаггард) По словам Уитни, эта неупакованная версия формулы Эйлера - невероятный инструмент. Например, это важно для разработки электроники, которая использует переменный ток или переменный ток. «Формула Эйлера в расширенной форме означает, что вы можете использовать сложные или мнимые числа для анализа и проектирования цепей переменного тока», - говорит Уитни. Это связано с тем, что в цепи переменного тока напряжение представляет собой величину, которая колеблется во времени - обычно 60 раз в секунду, например, при стандартном электропитании в США. «Полная версия формулы Эйлера учит, как мы можем использовать комплексные числа в качестве удобного сокращения для моделирования колебательных явлений», - говорит Уитни.
Полевые уравнения Эйнштейна
Основные компоненты его общей теории относительности, уравнения поля Альберта Эйнштейна, описывают, как гравитация от массы и энергии создает искривление пространства-времени.
(Иллюстрация Виктории Джаггард) «Описание этой кривизны включает в себя геометрию, и поскольку первоначальное определение числа« пи »происходит от геометрии, его появление в этом уравнении не так уж удивительно», - говорит Ливио. В дополнение к раскрытию фундаментальной истины о том, как работает вселенная, общая теория относительности имеет много практических применений. Например, спутники, составляющие Глобальную систему позиционирования, используемые для навигации, будут безнадежно не синхронизированы друг с другом, если инженеры не учтут эффекты замедления времени, предсказанные теорией.
